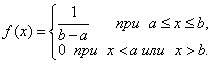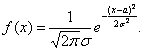Тема 1: Основные понятия теории вероятностей

 

Литература

 

1. Вентцель Е.С. Теория вероятностей. м.: Наука. 1969. С. 23-36.

2. Эддоус М., Стэнсфилд Р. Методы принятия решений. М.: «Аудит», издательское объединение «ЮНИТИ», 1997. С. 10-15.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая
школа, 1977. С. 7-15.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1999. С. 8-18.

 

__________________________________________________

Содержание теоретического минимума

__________________________________________________

 

1. Элементы комбинаторики.

2. Понятие события.

3. Вероятность события (классическое определение вероятности).

4. Случайные события как подмножества множества простейших исходов.

_____________________________________

Краткие теоретические сведения

 

1. Элементы комбинаторики

Перестановкой называется определенное линейное расположение всех элементов некоторого множества. Число перестановок из n элементов обозначается  и равно

Размещением называется любой набор, содержащий m элементов этого множества, взятый в определенном линейном порядке. Число размещений  из n элементов по  m обозначается  и равно:

Сочетанием называется любой набор, содержащий m элементов этого множества, без учета их порядка. Число размещений из n элементов по m обозначается и равно:

 

2. Понятие события

Событие- всякий факт, который в результате опыта может произойти или не произойти.

Достоверным называют событие , которое обязательно произойдет, если будет осуществлена определенная совокупность условий S .

Невозможным называют событие , которое заведомо не  произойдет, если будет осуществлена определенная совокупность условий S .

Случайным называют событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти.

Несколько событий образуют полную группу событий в данном опыте, если в результате опыта непременно должно появиться хотя бы одно из них.

Несколько событий называют несовместными в данном опыте, если никакие два из них не могут появиться вместе.

Несколько событий называют равновозможными в данном опыте, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое.

События, которые обладают всеми тремя свойствами: образуют полную группу, несовместны и равновозможны называют элементарными исходами (элементарными событиями) или случаями.

Элементарный исход, который ведет к появлению события А, называют благоприятным исходом событию А. Событие A можно рассматривать как набор благоприятных ему исходов.

Множество всех элементарных исходов называют полным пространством событий и обозначают буквой.

 

3.Вероятность события (классическое определение вероятности)

Вероятность события - численная мера объективной возможности этого события.

Вероятность события А  (если опыт сводится к схеме случаев) определяется формулой          (классическая формула вероятности),

где n- общее число элементарных исходов,

m- число благоприятных исходов событию А.

Так как  m  заключено между 0 и n, то .

Вероятность достоверного события , так как m=n.

Вероятность невозможного события равна 0, так как m=0.

 

4.Случайные события как подмножества множества  простейших исходов.

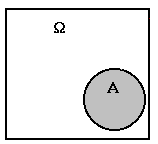
Представление о пространстве событий, называется диаграммами Венна.

 

           Рассмотрим квадрат со стороной равной единице. Будем считать, что множество всех точек квадрата соответствует совокупности элементарных событий . При этом каждое отдельное элементарное событие    это некоторое

подмножество точек данного квадрата. Тогда любая фигура A, составленная из таких подмножеств, будет изображать некоторое событие, а ее площадь можно считать вероятностью этого события. Разумеется, вероятность всего пространства элементарных  событий совпадает с площадью квадрата и равна единице. Событие, которое никогда не сбывается, не содержит ни одной точки из этого пространства элементарных событий и имеет вероятность и, следовательно, площадь равную нулю.

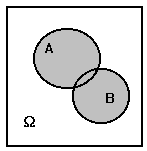
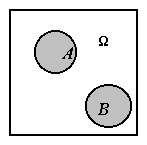
Если события А и В несовместны, то происхождение одного исключает происхождение другого. Это означает, что эти события не имеют общих элементарных исходов, т.е. множества А и В не пересекаются. На диаграмме это выглядит следующим образом:

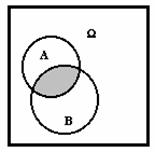
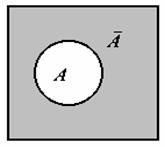
Событие С называют противоположным событию А, если события А и С несовместны и их суммой будет все пространство элементарных событий. Противоположное к А событие будем обозначать . На языке множеств противоположным к  А событием будет являться дополнение к А, т.е. все, что не вошло в событие А.

На диаграмме это выглядит следующим образом:

 

_________________________________

Примеры решений типовых задач

 

Задача 1. Один раз подбрасывается игральная кость. Построить пространство элементарных исходов. Описать события:

 - появление не более 2-х очков;

 - появление 3-х или 4-х очков;

 - появление не менее 5 очков;

 -появление четного количества очков.

Есть ли среди этих событий равновозможные? Указать, какие из этих событий несовместны, какие совместны, какие образуют полную группу?

Решение. Пространство элементарных исходов состоит из следующих элементарных событий
.

Опишем указанные события:      

События  - равновозможные, так как им благоприятствует равное число элементарных исходов (по два исхода).

События   попарно несовместны, так как у них нет общих элементарных исходов.

События  и ,   и,  и  совместны, так как у них есть общие элементарные исходы.

События  и  образуют полные группы

Задача 2. В ящике находятся 10 деталей, из которых 4 - бракованных. Наудачу извлечены 3 детали. Найти вероятность того, что среди извлеченных деталей: а) нет годных; б) нет бракованных; в) одна бракованная две годных.

Решение. Общее число возможных элементарных исходов испытания во всех трех случаях равно числу способов, которым можно извлечь 3 детали из 10, т.е. равно числу сочетаний из 10 элементов по 3:  . Число исходов, благоприятствующих интересующему нас событию, равно: а) числу способов, которым можно извлечь 3 детали из 4 бракованных деталей, т.е. ; б) числу способов, которым можно извлечь 3 детали из оставшихся 6 годных деталей, т.е. ; в) в этом случае каждый из способов, которым можно извлечь из 4 бракованных деталей одну, сочетается со способом, которым можно извлечь 2 годных детали из 6, т.е.  Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу элементарных исходов:

а); б); в).

Задача 3. Брошены две игральные кости. Какова вероятность того, что сумма очков на выпавших гранях делится на два, причем на грани хотя бы одной из костей появится 1?

Решение. На выпавшей грани одной из костей может появиться 1,2,...,6 очков. Аналогично появление 6 граней возможно при бросании другой кости. Каждый из исходов бросания одной кости может сочетаться с каждым из исходов бросания другой. Следовательно, общее число элементарных исходов испытания n=66=36. Исходы, благоприятствующие интересующему нас событию:

1 кость

1

1

1

3

5

2 кость

5

3

1

1

1

Отсюда m=5. Искомая вероятность равна  .

Задача 4. На каждом кубике написана буква и из них сложено слово “ ЗАДАЧА ”. Кубики рассыпаны и снова сложены с ряд. Какова вероятность того, что вновь получено прежнее слово?

Решение. Общее число возможных исходов испытания равно числу способов, которыми можно переставить 6 букв, т.е.  Число исходов, благоприятствующих интересующему нас слову, равно числу способов, которыми можно переставить повторяющиеся буквы, т.е.  Искомая вероятность 

Задача 5. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Какова вероятность правильно набрать номер?

Решение. Общее число возможных исходов испытания равно числу размещений из пяти цифр по две, так как нечетных цифр пять (1,3,5,7,9), а забыто абонентом две цифры, т.е.  Число исходов, благоприятствующих правильному набору телефонного номера, равно m=1. Искомая вероятность будет равна

Задача 6. Из трех бухгалтеров, восьми менеджеров шести научных сотрудников необходимо случайным отбором сформировать комитет из десяти человек. Какова вероятность того, что в комитете окажутся: один бухгалтер, пять менеджеров и четверо научных сотрудников?

Решение. Общее число возможных комитетов равно числу сочетаний из 17 по 10 человек, т. е.

Число исходов, благоприятствующих формированию нужного комитета равно

Следовательно, итоговая вероятность формирования комитета заданного состава равна:

______________________________________

Задачи для самостоятельного решения

1. Три раза подбрасывается монета. Построить пространство элементарных исходов. Описать события:

 - герб выпал один раз;

 - герб выпал по крайней мере один раз;

 -герб не выпал ни разу;

 - герб выпал менее двух раз.

Есть ли среди этих событий равновозможные? Указать, какие из этих событий несовместны, какие совместны, какие образуют полную группу?

2. В транспортной компании работают 10 водителей. На каждый из пяти обслуживаемых через день заводов требуется послать одного из водителей. Сколькими способами это может быть осуществлено?

3. Каждую пятницу бронированный автомобиль доставляет заработную плату из местного отделения банка в пять фирм. В качестве меры предосторожности стараются использовать различные маршруты. Водитель выбирает из предложенных диспетчером вариантов. Какова вероятность того, что нынешний маршрут не повторит предыдущий? Какова вероятность того, что маршрут не повторится ни разу в течение месяца?

4. Слово "институт" разрезали на буквы. Эти буквы перемешали и наудачу выложили в ряд. Какова вероятность снова получить слово "институт"? Как изменится вероятность, если очередная буква записывается и возвращается к остальным?

5. Среди 100 изделий 20 – бракованных. Найти вероятность того, что среди наудачу отобранных 10 изделий бракованных 3.

6. 12 студентов случайным образом занимают очередь за стипендией. Найти вероятность того, что между Ивановым и Петровым будет стоять ровно 5 человек.

7. В ящике лежат 15 красных, 9 синих и 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что среди них 1 зеленый, 2 синих и 3 красных шара.

__________________________

Индивидуальные задания

1. 6 человек случайным образом рассаживаются за круглым столом. Найти вероятность того, два фиксированных лица A и B окажутся рядом.

2. Студент знает ответы на 20 вопросов из 25. Билеты составлены из всех 25 вопросов по 3 вопроса в билете. Какова вероятность того, что студент ответит на все вопросы из доставшегося ему билета.

3. 10 книг случайным образом расставляют на полке. Какова вероятность, что две фик­си­рованные книги окажутся рядом?

4. 5 шариков случайным образом разбрасываются по 8 лункам. Какова вероятность того, что в первых пяти лунках будет ровно по одному шару?

5. Буквенный замок содержит на общей оси 5 дисков, каждый из которых разделен на 6 секторов с различными буквами. Замок открывается толь в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Определить вероятность открытия замка, если установлена произвольная комбинация букв.

6. На курсах повышения бухгалтеров учат определять правильность накладной. В качестве проверки преподаватель предлагает учащимся проверить 10 накладных, 4 из которых содержат ошибки. Он берет наугад из этих 10 две накладные и просит проверить. Какова вероятность того, что они окажутся: а) обе ошибочные; б) одна ошибочная, а другая нет?

При условии, что учащийся идентифицирует неправильную накладную с вероятностью 0,9, какова вероятность правильной идентификации двух предложенных ему накладных, если а) обе ошибочные; б) одна ошибочная, а другая нет?

 

Место для решения задач

Тема 2: Теоремы теории вероятностей

 

Литература

 

1. Вентцель Е.С. Теория вероятностей. м.: Наука. 1969. С. 37-66.

2. Эддоус М., Стэнсфилд Р. Методы принятия решений. М.: «Аудит», издательское объединение «ЮНИТИ», 1997. С. 16-25.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая
школа, 1977. С. 17-47.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1999. С. 18-39.

 

 

____________________________________

Содержание теоретического минимума

____________________________________

 

1. Сумма и произведение событий.

2. Условная вероятность.

2. Теорема сложения и следствия из нее.

3. Теорема умножения и следствия из нее.

4. Формула полной вероятности. Теорема Байеса.

5. Формула Бернулли.

_____________________________________

Краткие теоретические сведения

 

1. Сумма и произведение событий.

Под суммой событий А и В

Следует понимать такое событие С, которое происходит, когда происходит или событие А, или В, или А и В вместе, т.е. если состоялось событие А, то состоялось и C; если состоялось событие В, то тоже состоялось C. На языке множеств, которые изображаются с помощью диаграмм Венна, сумме событий А и В будет соответствовать объединение множеств А и В. Обозначается C=A+B

Под произведением событий A и B  будет пониматься такое событие C, которое состоит из элементарных событий А и В одновременно, т.е. произведению событий будет соответствовать пересечение множеств А и В. Обозначается C=AB

Если события A и В несовместны, то АВ=.

 

2. Условная вероятность.

Событие А называется независимым от события В, если вероятность событие А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Условной вероятностью P(A/B) называется вероятность события A при условии, что B уже произошло.

В классическом случае

,

где  - число исходов, благоприятных одновременно событиям А и В,  

 - число исходов, благоприятных событию В.

Легко видеть, что, разделив числитель и знаменатель дроби на общее число исходов n, получим

.

Последнее равенство в общем случае принимается в качестве определения.

Условие независимости событий можно записать  формулой , а условие зависимости формулой .

3. Теорема сложения и следствия из нее.

Т1 (о сложении вероятностей несовместных событий). Вероятность суммы события A и несовместного с ним события B равна сумме вероятностей событий A и B.

P(A+B)=P(A)+P(B).

Следствие 1. Вероятность P() противоположного к A события равна 1 — P(A):

P() = 1 — P(A).

Следствие 2.  Если события   несовместны и   - достоверное событие, то .

Т2 (о сложении вероятностей совместных событий). Вероятность суммы событий A и B равна сумме вероятностей каждого из событий  минус вероятность их произведения

P(A+B)=P(A)+P(B)-P(AB).

 

4.Теорема произведения и следствия из нее.

Т3. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

.

При применении теоремы безразлично, какое событие считать первым, какое вторым:

Следствие1 (Т3) . Если событие А не зависит от события В, то и событие В не зависит от события А.

Следствие2 (Т3) . Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

.

4. Формула полной вероятности.

Т(4). Предположим, что все множество элементарных событий разбито на конечное число k несовместных событий Н1, ..., Нk, т.е. . Тогда,  вероятность события А будет складываться из пересечений события А и каждого из Нi , т.е.

P(А) =.

называется системой гипотез.

Теорема Байеса.

Т5. Если в результате эксперимента, пространство элементарных исходов которого разбивается системой гипотез , произошло событие А, то вероятности гипотез могут быть переоценены:

 .

5. Формула Бернулли.

Несколько испытаний называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания.

Т6. Если вероятность р появления события А постоянна в каждом испытании,  то вероятность  того, что событие А появится в n независимых испытаниях ровно m раз, равна

.

________________________________

Примеры решений типовых задач

 

Задача 1. При проверке документа можно обнаружить четыре нарушения в его оформлении. Рассматриваются события: А - обнаружено ровно одно нарушение; В - обнаружено хотя бы одно нарушение; С - обнаружено не менее 2-х нарушений; D - обнаружено ровно два нарушения; E - обнаружено ровно 3 нарушения; F - обнаружены все нарушения. Указать в чем состоят события:

а)  А+В;  б) АВ;  в) ВС;  г)  В+С;  д) D+E+F;  e) DF.

Решение.  а)  А  В, поэтому  А+В = В;

                  б) А  В, поэтому  АВ = A;

                   в) С В, поэтому ВС=С;

                   г) С В, поэтому В+С=В;

                   д) D F, E  F, поэтому D+E+F=F;

                   е) D F, поэтому DF=D.

Задача 2. На стеллаже библиотеки в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 2 учебника. Найти вероятность того, что:  а) первый учебник будет в переплете (событие А); б) второй учебник будет в переплете (событие В);  в) два учебника будут в переплете (событие С);  г)  хотя бы один учебник будет в переплете (событие D).

Решение. а) Вероятность события А равна отношению числа случаев, благоприятных событию А, к числу всех возможных, т.е. Р(А)=.

б) Второй учебник может быть в переплете в двух случаях: если событие А произойдет или событие А не произойдет (событие ). Вероятность того, что второй учебник имеет переплет при условии, что первый взятый учебник был в переплете, т.е. условная вероятность события В равна  вероятность, что второй учебник имеет переплет при условии, что первый взятый учебник был без переплета равна . Искомая вероятность, по теореме сложения несовместных событий (Т1), равна

.

в) Событие С состоит в произведении событий А и В, причем событие В зависит от того, произошло ли событие А. По тереме умножения вероятностей зависимых событий (Т3)

.

г) Событие D противоположно событию “ ни одного учебника не будет в переплете, т.е. событию, которое является произведением событий “ первый учебник без переплета” -  и “ второй учебник без переплета” - , т.е. . По теореме умножения зависимых событий (Т3)   .

Вероятность противоположного событию А события . Вероятность того, что второй учебник будет без переплета при условии, что первый тоже был без переплета: , т.е.    . Отсюда .

Задача 3. В ящике имеется 10 одинаковых деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает деталь, записывает цвет и возвращает деталь в ящик. Найти вероятность того, что три извлеченные детали окажутся окрашенными.

Решение. Пусть  - события, заключающиеся в том, что первая, вторая, третья деталь соответственно окажутся окрашенными. Интересующее нас событие состоит в совмещении событий , т.е. . Поскольку извлеченные детали возвращались обратно, события  - независимы. По теореме умножения независимых событий (следствие 2 (Т3)):

Задача 4. Решить предыдущую задачу, если извлеченные детали обратно не возвращались.

Решение. Применим обозначения предыдущей задачи. В новых условиях  - зависимы, поскольку вероятность вынуть следующую окрашенную деталь зависит от того, была ли уже извлечена одна окрашенная. По теореме умножения зависимых событий (Т3):

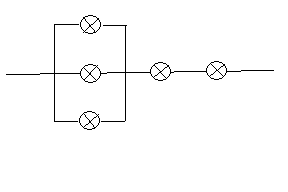
2
 

5
 

4
 

3
 

1
 
Задача 6. Схема прибора, пропускающего сигналы, содержит 5 элементов (см. черт. 1). Вероятность отказа в работе для 1-го, 2-го, 3-го, 4-го, 5-го
элементов раны соответственно:  Определить надежность работы прибора.

Решение. Обозначим надежность работы прибора, т. е. вероятность того, что ток пройдет через весь прибор - . Сигнал пройдет через участок с параллельным включением (событие ), если будет работать хотя бы один из элементов этого участка, т.е. надежность этого участка .

Событие А состоит в совмещении событий  и безотказной работы 4-го и 5-го элементов, т.е. надежность всей системы:

.

Задача 6. В первой партии из 60 изделий содержится 8 дефектных, во второй партии из 40 деталей содержится 4 дефектных. Из первой партии взяли 10 деталей, из  второй 6, перемешали и взяли одно изделие. Найти вероятность того, что взятое изделие дефектное (событие А).

Решение. Пусть  - гипотеза, состоящая в том, что изделие принадлежит первой партии.

 - гипотеза, состоящая в том, что изделие принадлежит второй партии. Очевидно, что . Вероятность того, что изделие, принадлежащее первой партии, дефектно равна . Если изделие принадлежит второй партии, то . По формуле полной вероятности (Т4):

.

Задача 7. Студент решает задачу по математике. С вероятностью 0,15 он неправильно перепишет условие задачи. Если он все же переписал его правильно, то с вероятностью 0,3 он выберет неправильный способ решения. Если он выбрал правильный способ решения, то с вероятностью 0,2 он допустит ошибку в вычислениях. Задача решена неверно. Какова вероятность того, что студент выбрал неправильный способ решения?

Решение. Пусть  - гипотеза, состоящая в том, что студент неправильно перепишет условие задачи.  - гипотеза, состоящая в том, что он правильно перепишет условие.  - событие, состоящее в том, что студент выберет неправильный способ решения.  - событие, состоящее в том, что студент допустит ошибку в вычислениях.  - событие, состоящее в том, что задача решена неправильно.

Рассмотрим первую гипотезу.

Очевидно, что . Вероятность того, что задача будет решена неправильно, равна .

Рассмотрим вторую гипотезу.

Если студент правильно переписал условие задачи, то вероятность выбора неправильного решения . В этом случае задача будет решена неправильно с вероятностью

Если студент правильно переписал условие задачи, вероятность выбрать правильный способ ее решения равна

Если студент правильно переписал условие задачи, выбрал правильный способ ее решения, то вероятность допустить ошибку в вычислениях равна  . В этом случае задача будет решена неправильно с вероятностью

Вероятность неправильного решения задачи при реализации второй гипотезы ровна

По формуле полной вероятности (Т4):

То есть

___________________________________

Задачи для самостоятельного решения

 

1. Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку, равна 0,1, второй - 0,15, третий - 0,2. Найти вероятность того, что при однократном измерении будет допущена ошибка хотя бы одним исследователем.

2. Из колоды в 52 карты наудачу извлекается 3 карты. Какова вероятность, что три карты красной масти, если среди них два туза.

3. Среди десяти документов три оформлены не по стандарту. Документы проверяют один за другим до выявления всех нестандартных. Какова вероятность того,  что проверка закончится на 5 документе.

4. Опечатки при наборе текста книги возникают с вероятностью 0,02. После набора книги распределяются по двум корректорам в соотношении 3:2. Первый корректор обнаруживает ошибку с вероятностью 0,9, второй - 0,85. Какова вероятность того, что книга выйдет с опечатками?

5. Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2,  0,4,  1,3.

6. Фирма собирается выпускать новый товар на рынок. Подсчитано, что вероятность хорошего сбыта продукции равна 0,6; плохого - 0,4. Компания собирается провести маркетинговое исследование, вероятность правильности которого 0,8. Как изменятся первоначальные вероятности уровня реализации, если это исследование предскажет плохой сбыт?

7. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются).

_________________________

Индивидуальные задания

1. Из колоды в 52 карты вынули 5 карт. Найти вероят­ность того, что:

     а)  все 5 карт одной масти;

     б)  среди этих 5 карт представлены все масти.

2. Студент знает ответы на 25 вопросов из 30. Найти веро­ятность того, что он ответит не на все вопросы из билета, в котором 3 вопроса.

3. Бросаются три кости. Найти вероятность того, что хотя бы на одной из них выпало одно очко, если известно, что на всех трех выпали разные грани.

4. Среди двенадцати ламп две неисправны. Лампы про­веряют одну за другой до выявления двух неисправных. Найти веро­ятность того, что проверка закончится на пятой лампе.

5. Из колоды вынули две карты, одну из них посмотрели - она оказалась тузом. Затем эти две карты перемешали между собой и вынули одну. Найти вероятность того, что это: а) снова туз; б) десятка.

6. Студент, разыскивая нужную ему книгу, решил обойти три библиотеки. Для каждой библиотеки одинаково вероятно, есть в ее фондах книга или нет. Если книга есть, то одинаково вероятно вы­дана она читателю или свободна. Найти вероятность того, что студент получит книгу.

7. Ошибка при индексировании документа возникает с вероятностью 0,01. После индексирования треть всех документов на­правляется в первый проверочный пункт, а две трети во второй. Пер­вый пункт пропускает ошибку с вероятностью 0,2, а второй - с вероят­ностью 0,3. Найти вероятность того, что документ попадет в архив с ошибкой в индексировании.

8. Проводится серия испытаний прибора, который при каждом испытании ломается с постоянной вероятностью p. После первой поломки прибор ремонтируют, после второй признают негод­ным. Найти вероятность того, что:

     а) прибор не будет признан негодным после пяти испытаний;

     б) прибор будет признан негодным на седьмом испытании.

9. Событие В наступит в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет проведено 5 независимых испытаний, в каждом из которых событие А наступает с вероятностью 0,8.

10. Под документом необходимо получить подписи руководителя учреждения или двух его заместителей. Руководитель даст согласие под­писать документ с вероятностью 0,5; первый заместитель - с вероятностью 0,3; второй - с вероятностью 0,9. Найти вероятность того, что нужное число подписей будет собрано.

11. В спартакиаде участвуют из первой группы 4 студента, из второй ‑ 6, из третьей ‑ 5. Студент из первой группы попадает в сборную института с вероятность 0,9, второй ‑ 0,7, третьей ‑ 0,8. Наудачу выбранный студент попал в сборную. Какова вероятность того, что это студент из второй группы.

12. Часы изготавливаются на трех заводах и поступают в магазин. Первый завод производит 40% продукции, второй ‑ 45%, третий ‑ 15%. В продукции первого завода спешат 30% часов, у второго ‑ 70%, у третьего ‑ 90%. Купленные часы спешат, какова вероятность, что они изготовлены на втором заводе?

13. Группа состоит из 5 отличников, 15 хорошо успевающих и 5 занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные отметки, хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные отметки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные отметки. Для сдачи наугад назван студент. Какова вероятность того, что он получит хорошую отметку?

Место для решения задач

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Замечания преподавателя

 

Тема 3: Случайные величины, способы их задания и числовые характеристики. Основные законы распределения.

 

Литература

 

1. Вентцель Е.С. Теория вероятностей. м.: Наука. 1969. С. 67-130.

2. Эддоус М., Стэнсфилд Р. Методы принятия решений. М.: «Аудит», издательское объединение «ЮНИТИ», 1997. С. 26-27, 38-70.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая
школа, 1977. С. 57-87, 105-132.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1999. С. 52-82, 87-119.

 

_____________________________________

Содержание теоретического минимума

____________________________________

 

1. Понятие случайной величины.

2. Ряд распределения дискретной случайной величины.

3. Функция распределения вероятностей случайной величины.

4.Плотность распределения вероятностей непрерывной случайной величины.

5.Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение.

6. Основные законы распределения случайных величин: биномиальное распределение, распределение Пуассона, равномерное распределение, нормальное распределение.

________________________________

Краткие теоретические сведения

 

1.Понятие случайной величины

Случайной называют величину, которая в результате испытания принимает одно из возможных своих значений, наперед неизвестное.

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т. е. между двумя соседними возможными значениями нет возможных значений), кото­рые эта величина принимает с определенными вероятностями. Дру­гими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной слу­чайной величины может быть конечным или бесконечным (в послед­нем случае множество всех возможных значений называют счетным).

Непрерывной называют случайную величину, возможные значения которой сплошь заполняют некоторый конечный или бесконечный интервал. Число возможных значений непрерывной случайной величины бесконечно.

 

2. Ряд распределения дискретной случайной величины


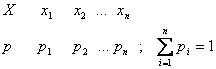
Рядом (законом) распределения дискретной случайной величины X называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины Х может быть. задан в виде таблицы, первая строка которой содержит возможные значения X, а вторая—вероятности р(X):

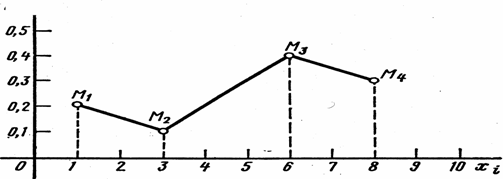
Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки — возможные значения X,  — соответствующие вероятности и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Например, дискретная случайная величина Х задана законом распределения:

X       1      3       6        8

P      0,2   0,1    0,4     0,3

Построим прямоугольную систему координат, по оси абсцисс будем откладывать возможные значения X, а по ординат — соответствующие вероятности р,. Построим точки . Соединив эти точки отрезками прямых, получим искомый, многоугольник распределения.

 


3. Функция распределения случайной величины

Функцией распределения называют функцию Р (х), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т. е.

F(х)=Р(Х<х).

Часто вместо термина «функция распределения» используют термин «интегральный закон распределения».

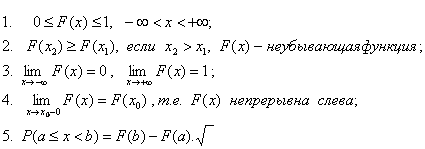
Функция распределения обладает следующими свойствами:

Для непрерывной случайной величины выполняется следующее свойство, называемое иногда «парадоксом нулевой вероятности»: P(X=a)=0 для любого конкретного числа а.

 

4. Плотность распределения вероятностей непрерывной случайной величины

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:


Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу , определяется равенством:

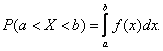
Зная плотность распределения, можно найти функцию распределения

 

 

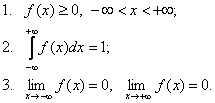
5. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение

Характеристикой среднего значения случайной величины служит математическое ожидание, которое определяется по формулам


Свойства математического ожидания (если свойство касается нескольких случайных величин, подразумевается, что они заданы на одном и том же пространстве элементарных исходов):


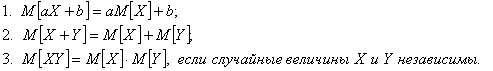
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Дисперсию удобно вычислять по формуле

Свойства дисперсии:

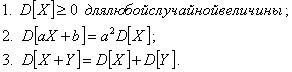
Средним квадратическим отклонением случайной величины называют квадратный корень из ее дисперсии:


6. Основные законы распределения

Биномиальное распределение

Дискретная случайная величина X, принимающая целочисленные значения
имеет биномиальное распределение, если вероятность значения k вычисляется по формуле Бернулли:

где 0<p<1,    q=1-p.

Биномиальный закон распределения имеет случайная величина, равная числу успехов в серии из  n независимых испытаний Бернулли с вероятностью успеха  p в каждом испытании.

Для биномиального распределения

Распределение Пуассона

Дискретная случайная величина X, принимающая положительные целочисленные значения  k , имеет распределене Пуассона, если вероятности ее значений вычисляются по формуле

Для распределения Пуассона

Теорема Пуассона.

 Эта теоре­ма дает пуассоновское приближение биномиального распределения и обычно используется при  p<0,1  и  npq9 .

Равномерное распределение

Непрерывная случайная величина X, принимающая значения на отрезке  имеет равномерное распределение, если плотность распределения вероятностей имеет вид

Для равномерного распределения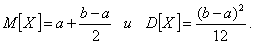

Нормальное распределение.

Непрерывная случайная величина X, принимающая значения на всей числовой прямой, имеет нормальное распределение с параметрами 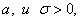 если плотность распределения вероятностей имеет вид

Для нормального распределения  

Вероятность попадания нормально распределенной случайной величины на отрезок  вычисляется по формуле 

 
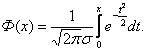
где Ф(х) – функция Лапласа, которая определяется равенством

Интегральная теорема Муавра – Лапласа

Если  то для случайной величины X

Теорема дает нормальное приближение биномиального распределения применяется при  p>0,1  и npq>9.

_________________________________

Примеры решений типовых задач

 

Задача 1. Вероятность поломки одного из пяти работающих независимо друг от друга станков равна 0,2. Если происходит поломка, станок до конца дня не работает. Какова вероятность, что  в течение дня сломается менее трех станков.

Решение.

X – число сломавшихся станков в день.

В данном случае присутствуют все условия биномиального распределения:

1.      Пять станков представляют собой пять идентичных опытов.

2.      Станки работают независимо друг от друга.

3.      Возможны два исхода для каждого из станков – или он ломается или нет.

4.      Вероятность поломки одинакова – 0,2.

Следовательно, вероятность бесперебойной работы равна – 0,8, отсюда вероятность менее трех поломок в течение дня:


Ожидаемое количество поломок в день:


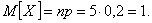
Дисперсия: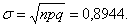

Среднее квадратическое отклонение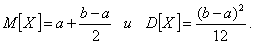

Задача 2. В среднем на телефонной станции заказывают шесть телефонных разговоров в течение десяти минут. Какова вероятность, что будет заказано ровно два разговора или хотя бы один разговор в течение пяти минут?

Решение.

X – количество разговоров, заказываемых в течение пяти минут.

Применим распределение вероятностей Пуассона, так как:

1.      Существует неограниченное количество опытов, т. е. маленьких отрезков времени, когда времени одинаково. может появиться заказ на телефонный разговор, вероятность чего мала и постоянна.

2.      Считается, что спрос на телефонные разговоры беспорядочно распределен во времени.

3.      Считается, что среднее число телефонных разговоров в любом 10 – минутном отрезке

В этом примере среднее число заказов равно 3 за 5 минут:

Отсюда:

Задача 3. Производители карманных калькуляторов знают из опыта, что 1% произведенных и проданных калькуляторов имеют дефекты и их должны заменить по гарантии. Большая аудиторская фирма купила 500 калькуляторов. Какова вероятность, что три или больше калькуляторов придется заменить?

Решение.

X-количество калькуляторов, которое придется заменить.

Ситуация прекрасно укладывается в рамки биномиального распределения.

Так как p <0,1, а npq<9, то в качестве замены биномиального распределения может быть использовано распределение Пуассона при m=5.

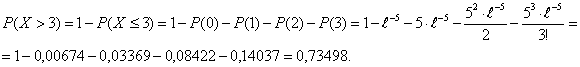
Задача 4. Бухгалтер тратит на дорогу на работу 20 – 25 минут. Любое время на дорогу в этих пределах равновероятно. Подсчитать вероятность того, что дорога на работу занимает у бухгалтера от 20,5 до 22,8 минут.

Решение.

X - время, которое бухгалтер тратит на дорогу на работу.

Так как вероятность полной группы событий строго равна 1, то и площадь под кривой плотности вероятности должна быть равна 1, Это правило облегчает подсчет плотности вероятности для равномерного распределения. Интервал времени 5 минут, значит, ширина прямоугольника равна 5, следовательно, его высота (плотность вероятности) должна быть 1/5, тогда площадь под кривой (1/5)*5=1.

Тогда   

Задача 5. Производителю электроламп известно, что средний срок работы лампы составляет 600 часов, а стандартное отклонение срока работы – 40 часов. Какова вероятность, что срок работы от 550 до 700 часов?

Решение. На рисунке площадь заштрихованного пространства равна вероятности того, что лампа проработает от 550 до 700 часов.

Так как Ф(х) – нечетная функция, то    Ф(-1.25)=-Ф(1.25).
По таблице нормального распределения находим:

Ф(2,5)=0.0.4938, а    Ф(1.25)=0.3944.

Таким образом, вероятность того, что электролампа проработает от 550 ч до
700 ч равна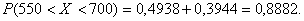   

Задача 6. Каждый день завод производит огромное количество чипсов, 40% из которых бракованные. Для проверки качества отбираются 100 образцов из произведенных за день чипсов. Какова вероятность, что 50 или больше из 100 бракованные?

Решение. Проверим, можно ли заменить биномиальное распределение нормальным:   .

Полученные результаты показывают, что применение нормального распределения в качестве приближения биномиального возможно.

Среднее нормального распределения: отклонения равно 40, стандартное отклонение равно:

.

Искомая вероятность будет равна:

 

____________________________________

Задачи для самостоятельного решения

1. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0.4, независимо от других магазинов. Найти вероятность того, что число заявок в день не превысит двух. Найти среднее число заявок в день.

2. При наборе книги на 200 страницах делают в среднем 5 опечаток. Найти вероятность того, что на 40 прочитанных страницах будет обнаружено не более трех опечаток.

3. Вероятность выпуска детали повышенной хрупкости 0,03. Детали упаковываются в коробки по 200 штук. Найти вероятность того, что в коробке окажется хотя бы одна деталь повышенной хрупкости.

4. Время ожидания поезда метро 0 – 2 мин. Любое время ожидания поезда в этих пределах равновероятно. Подсчитать вероятность того, что в очередной раз придется ждать от 1,25 до 1,75 минут. Сколько в среднем уходит на ожидание поезда метро за 30 дней у человека, пользующегося метро 2 раза в день?

5. Заряд охотничьего пороха отвешивается на весах, имеющих среднюю квадратическую ошибку взвешивания 150 мг. Номинальный вес порохового заряда 2.3 г. Определить вероятность повреждения ружья, если максимально допустимый вес порохового заряда 2.5 г.

6. Концертный зал, рассчитанный на 1200 мест, имеет четыре буфета. Каждый зритель с равной вероятностью может посетить любой из буфетов. На сколько мест должен быть рассчитан каждый буфет, чтобы с вероятностью 0.9 каждый зритель мог быть обслужен в том буфете, который он посетил?

___________________________

Индивидуальные задания

1. Имеется 5 станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Перерыв связи с каждой из станций происходит независимо от остальных с вероятностью p=0,2. Найти вероятность того, что в данный момент времени связь будет не более чем с двумя станциями.

2. На ткацком станке нить обрывается в среднем 0,375 раза в течение часа работы станка. Найти вероятность того, что за 8 часовую смену число обрывов нити будет не менее двух и не более четырех.

3. По некоторой цели производится 50 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,04. Найти вероятность того, что в цель попадет хотя бы один снаряд.

4. На изготовление детали рабочему требуется 20 – 25 мин. Любое время на изготовление в этих пределах равновероятно. Найти вероятность того, что на изготовление очередной детали потребуется от 23 до 25 мин.?

5. Ошибка прогноза температуры воздуха, есть случайная величина с m =0, s =2°. Найти вероятность того, что в течение недели ошибка прогноза трижды превысит по абсолютной величине 4°.

6. В архив поступают материалы по двум основным тематикам, причем по первой вдвое больше, чем по второй. Найти вероятность того, что из 2000 документов на первой тематике окажется больше 1500.

7. В библиотеке имеются книги только по технике и математике. Вероятность того, что любой читатель возьмет книгу по технике - 0.7, по математике - 0.3. Определить вероятность того, что из пяти читателей книгу по математике возьмут не менее трех, если каждый читатель берет только одну книгу.

8. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени 15 секунд испускало в среднем 7.5 a-частиц. Найти вероятность того, что за 2 секунды это вещество испустит хотя бы одну a-частицу.

9. Вероятность того, что изделие не выдержит испытание, равна 0.001. Найти вероятность того, что из 5000 изделий испытание не выдержат менее двух изделий.

10. На обработку одного документа сотруднику требуется  30 – 40 мин. Любое время на обработку в этих пределах равновероятно. Какова вероятность того, что на обработку очередного документа придется затратить от 33 до 35 мин.?

11. Изделие считается высшего качества, если отклонение его размеров от номинала не превосходит по абсолютной величине 3.45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону со средним квадратичным отклонением s=3 мм.  Изготовлено 4 изделия. Какова вероятность того, что среди них хотя бы одно изделие не высшего качества?

12.В кафе самообслуживания 90 мест. Его обслуживают 3 кассы. Найти вероятность того, что в одну из касс выстроится очередь более чем из 35 человек.

 

Место для решения задач

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Замечания преподавателя